Формула нахождения дисперсии. Математическое ожидание и дисперсия случайной величины

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для вычисления дисперсии можно использовать слегка преобразованную формулу

так как М(Х) , 2 и
– постоянные величины. Таким образом,

4.2.2. Свойства дисперсии

Свойство 1. Дисперсия постоянной величины равна нулю. Действительно, по определению

Свойство 2. Постоянный множитель можно выносить за знак дисперсии с возведением его в квадрат.

Доказательство

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:

Центрированная величина обладает двумя удобными для преобразования свойствами:

Свойство 3. Если случайные величины Х иY независимы, то

Доказательство . Обозначим
. Тогдаи.

Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин

Пример 4.5. Еслиa иb – постоянные, тоD(a Х+ b )= D (a Х)+ D (b )=
.

4.2.3. Среднее квадратическое отклонение

Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ , то дисперсия имеет размерность
. Поэтому часто предпочитают пользоваться другой характеристикой разброса –средним квадратическим отклонением , которое равно корню квадратному из дисперсии

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Пример 4.6. Дисперсия числа появления события в схеме независимых испытаний

Производится n независимых испытаний и вероятность появления события в каждом испытании равнар . Выразим, как и прежде, число появления событияХ через число появления события в отдельных опытах:

Так как опыты независимы, то и связанные с опытами случайные величины независимы. А в силу независимостиимеем

Но каждая из случайных величин имеет закон распределения (пример 3.2)

и
(пример 4.4). Поэтому, по определению дисперсии:

где q =1- p .

В итоге имеем
,

Среднее квадратическое отклонение числа появлений события в n независимых опытах равно
.

4.3. Моменты случайных величин

Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.

Начальным моментом k Х (
) называется математическое ожиданиеk -й степени этой случайной величины.

Центральным моментом k -го порядка случайной величиныХ называется математическое ожиданиеk -ой степени соответствующей центрированной величины.

Легко видеть, что центральный момент первого порядка всегда равен нулю, центральный момент второго порядка равен дисперсии, так как .

Центральный момент третьего порядка дает представление об асимметрии распределения случайной величины. Моменты порядка выше второго употребляются сравнительно редко, поэтому мы ограничимся только самими понятиями о них.

4.4. Примеры нахождения законов распределения

Рассмотрим примеры нахождения законов распределения случайных величин и их числовых характеристик.

Пример 4.7.

Составить закон распределения числа попаданий в цель при трех выстрелах по мишени, если вероятность попадания при каждом выстреле равна 0,4. Найти интегральную функцию F (х) для полученного распределения дискретной случайной величиныХ и начертить ее график. Найти математическое ожиданиеM (X ) , дисперсиюD (X ) и среднее квадратическое отклонение
(Х ) случайной величиныX .

Решение

1) Дискретная случайная величина Х – число попаданий в цель при трех выстрелах – может принимать четыре значения:0, 1, 2, 3 . Вероятность того, что она примет каждое из них, найдем по формуле Бернулли при:n =3,p =0,4,q =1- p =0,6 иm =0, 1, 2, 3:

Получим вероятности возможных значений Х :;

Составим искомый закон распределения случайной величины Х :

Контроль: 0,216+0,432+0,288+0,064=1.

Построим многоугольник распределения полученной случайной величины Х . Для этого в прямоугольной системе координат отметим точки (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). Соединим эти точки отрезками прямых, полученная ломаная и есть искомый многоугольник распределения (рис. 4.1).

2) Если х0, то F (х) =0. Действительно, значений, меньших нуля, величина Х не принимает. Следовательно, при всех х 0 , пользуясь определениемF (х) , получим F (х) =P (X < x ) =0 (как вероятность невозможного события).

Если 0, тоF (X ) =0,216. Действительно, в этом случаеF (х) =P (X < x ) = =P (- < X0)+ P (0< X < x ) =0,216+0=0,216.

Если взять, например, х =0,2, тоF (0,2)=P (X <0,2) . Но вероятность событияХ <0,2 равна 0,216, так как случайная величинаХ лишь в одном случае принимает значение меньшее 0,2, а именно0 с вероятностью 0,216.

Если 1, то

Действительно, Х может принять значение 0 с вероятностью 0,216 и значение 1 с вероятностью 0,432; следовательно, одно из этих значений, безразлично какое,Х может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,648.

Если 2, то рассуждая аналогично, получимF (х) =0,216+0,432 + + 0,288=0,936. Действительно, пусть, например,х =3. ТогдаF (3)=P (X <3) выражает вероятность событияX <3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функцииF (х) .

Если x >3, тоF (х) =0,216+0,432+0,288+0,064=1. Действительно, событиеX
является достоверным и вероятность его равна единице, аX >3 – невозможным. Учитывая, что

F (х) =P (X < x ) =P (X3) + P (3< X < x ) , получим указанный результат.

Итак, получена искомая интегральная функция распределения случайной величины Х:

F (x ) =

график которой изображен на рис. 4.2.

3) Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных значений Х на их вероятности:

М(Х) =0=1,2.

То есть, в среднем происходит одно попадание в цель при трех выстрелах.

Дисперсию можно вычислить, исходя из определения дисперсии D (X )= M (X - M (X )) или воспользоваться формулойD (X )= M (X
, которая ведет к цели быстрее.

Напишем закон распределения случайной величины Х:

Найдем математическое ожидание для Х :

М(Х) = 04
= 2,16.

Вычислим искомую дисперсию:

D (X ) = M (X) – (M (X )) = 2,16 – (1,2)= 0,72.

Среднее квадратическое отклонение найдем по формуле

(X ) =
= 0,848.

Интервал (M - ; M + ) = (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал наиболее вероятных значений случайной величиныХ , в него попадают значения 1 и 2.

Пример 4.8.

Дана дифференциальная функция распределения (функция плотности) непрерывной случайной величины Х :

f (x ) =

1) Определить постоянный параметр a .

2) Найти интегральную функцию F (x ) .

3) Построить графики функций f (x ) иF (x ) .

4) Найти двумя способами вероятности Р(0,5< X1,5) иP (1,5< X <3,5) .

5). Найти математическое ожидание М(Х) , дисперсиюD (Х) и среднее квадратическое отклонение
случайной величиныХ .

Решение

1) Дифференциальная функция по свойству f (x ) должна удовлетворять условию
.

Вычислим этот несобственный интеграл для данной функции f (x ) :

Подставляя этот результат в левую часть равенства, получим, что а =1. В условии дляf (x ) заменим параметра на 1:

2) Для нахождения F (x ) воспользуемся формулой

.

Если х
, то
, следовательно,

Если 1
то

Если x>2, то

Итак, искомая интегральная функция F (x ) имеет вид:

3) Построим графики функций f (x ) иF (x ) (рис. 4.3 и 4.4).

4) Вероятность попадания случайной величины в заданный интервал (а, b ) вычисляется по формуле
, если известнафункция f (x ), и по формуле P (a < X < b ) = F (b ) – F (a ), если известна функция F (x ).

Найдем
по двум формулам и сравним результаты. По условиюа=0,5; b =1,5; функцияf (X ) задана в пункте 1). Следовательно, искомая вероятность по формуле равна:

Та же вероятность может быть вычислена по формуле b) через приращение полученной в п.2). интегральной функцииF (x ) на этом интервале:

Так какF (0,5)=0.

Аналогично находим

так как F (3,5)=1.

5) Для нахождения математического ожидания М(Х) воспользуемся формулой
Функцияf (x ) задана в решении пункта 1), она равна нулю вне интервала (1,2]:

Дисперсия непрерывной случайной величиныD (Х) определяется равенством

, или равносильным равенством


.

ДлянахожденияD (X ) воспользуемся последней формулой и учтем, что все возможные значенияf (x ) принадлежат интервалу (1,2]:

Среднее квадратическое отклонение
=
=0,276.

Интервал наиболее вероятных значений случайной величины Х равен

(М-
,М+
) = (1,58-0,28; 1,58+0,28) = (1,3; 1,86).

Дисперсия в статистике находится как индивидуальных значений признака в квадрате от . В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

где n — частота (повторяемость фактора Х)

Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

Формулу дисперсии можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии , вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i - величина интервала;
А - условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

(если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi - групповая средняя;
ni - число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную , т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Наряду с изучением вариации признака по всей по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.
Выделяют дисперсию общую, межгрупповую и внутригрупповую .
Общая дисперсия σ 2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию, .

Межгрупповая дисперсия (δ) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
.

Внутригрупповая дисперсия (σ) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она вычисляется по формуле:
.

Средняя из внутригрупповых дисперсий : .

Существует закон, связывающий 3 вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии: .
Данное соотношение называют правилом сложения дисперсий .

В анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии. Он носит название эмпирического коэффициента детерминации (η 2): .
Корень квадратный из эмпирического коэффициента детерминации носит название эмпирического корреляционного отношения (η) :
.
Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1.
Покажем его практическое использование на следующем примере (табл. 1).

Пример №1 . Таблица 1 - Производительность труда двух групп рабочих одного из цехов НПО «Циклон»

Рассчитаем общую и групповые средние и дисперсии:




Исходные данные для вычисления средней из внутригрупповых и межгрупповой дисперсии представлены в табл. 2.
Таблица 2
Расчет и δ 2 по двум группам рабочих.


Группы рабочих 		Численность рабочих, чел. Средняя, дет./смен. Дисперсия

Прошедшие техническое обучение

5 95 42,0

Не прошедшие техническое обучение

5 81 231,2

Все рабочие

10 88 185,6
Рассчитаем показатели. Средняя из внутригрупповых дисперсий:
.
Межгрупповая дисперсия

Общая дисперсия:
Таким образом, эмпирическое корреляционное соотношение: .

Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Такое изучение вариации достигается посредством вычисления следующих видов дисперсий:

Внутригрупповая дисперсия доли определяется по формуле

где n i – численность единиц в отдельных группах.
Доля изучаемого признака во всей совокупности, которая определяется по формуле:
Три вида дисперсии связаны между собой следующим образом:
.

Это соотношение дисперсий называется теоремой сложения дисперсий доли признака.

Математическим ожиданием (средним значением) случайной величины X , заданной на дискретном вероятностном пространстве, называется число m =M[X]=∑x i p i , если ряд сходится абсолютно.

Назначение сервиса . С помощью сервиса в онлайн режиме вычисляются математическое ожидание, дисперсия и среднеквадратическое отклонение (см. пример). Кроме этого строится график функции распределения F(X) .

Свойства математического ожидания случайной величины

  1. Математическое ожидание постоянной величины равно ей самой: M[C]=C , C – постоянная;
  2. M=C M[X]
  3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M=M[X]+M[Y]
  4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M=M[X] M[Y] , если X и Y независимы.

Свойства дисперсии

  1. Дисперсия постоянной величины равна нулю: D(c)=0.
  2. Постоянный множитель можно вынести из-под знака дисперсии, возведя его в квадрат: D(k*X)= k 2 D(X).
  3. Если случайные величины X и Y независимы, то дисперсия суммы равна сумме дисперсий: D(X+Y)=D(X)+D(Y).
  4. Если случайные величины X и Y зависимы: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
  5. Для дисперсии справедлива вычислительная формула:
    D(X)=M(X 2)-(M(X)) 2

Пример . Известны математические ожидания и дисперсии двух независимых случайных величин X и Y: M(x)=8 , M(Y)=7 , D(X)=9 , D(Y)=6 . Найти математическое ожидание и дисперсию случайное величины Z=9X-8Y+7 .
Решение. Исходя из свойств математического ожидания: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23.
Исходя из свойств дисперсии: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345

Алгоритм вычисления математического ожидания

Свойства дискретных случайных величин: все их значения можно перенумеровать натуральными числами; каждому значению сопоставить отличную от нуля вероятность.
  1. Поочередно умножаем пары: x i на p i .
  2. Складываем произведение каждой пары x i p i .
    Например, для n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Функция распределения дискретной случайной величины ступенчатая, она возрастает скачком в тех точках, вероятности которых положительны.

Пример №1 .

x i 1 3 4 7 9
p i 0.1 0.2 0.1 0.3 0.3

Математическое ожидание находим по формуле m = ∑x i p i .
Математическое ожидание M[X] .
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
Дисперсию находим по формуле d = ∑x 2 i p i - M[x] 2 .
Дисперсия D[X] .
D[X] = 1 2 *0.1 + 3 2 *0.2 + 4 2 *0.1 + 7 2 *0.3 + 9 2 *0.3 - 5.9 2 = 7.69
Среднее квадратическое отклонение σ(x) .
σ = sqrt(D[X]) = sqrt(7.69) = 2.78

Пример №2 . Дискретная случайная величина имеет следующий ряд распределения:

Х -10 -5 0 5 10
р а 0,32 2a 0,41 0,03
Найти величину a , математическое ожидание и среднее квадратическое отклонение этой случайной величины.

Решение. Величину a находим из соотношения: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0.76 + 3 a = 1 или 0.24=3 a , откуда a = 0.08

Пример №3 . Определить закон распределения дискретной случайной величины, если известна её дисперсия, причем х 1 x 1 =6; x 2 =9; x 3 =x; x 4 =15
p 1 =0,3; p 2 =0,3; p 3 =0,1; p 4 =0,3
d(x)=12,96

Решение.
Здесь надо составить формулу нахождения дисперсии d(x) :
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
где матожидание m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Для наших данных
m(x)=6*0,3+9*0,3+x 3 *0,1+15*0,3=9+0.1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0.1x 3) 2
или -9/100 (x 2 -20x+96)=0
Соответственно надо найти корни уравнения, причем их будет два.
x 3 =8, x 3 =12
Выбираем тот, который удовлетворяет условию х 1 x 3 =12

Закон распределения дискретной случайной величины
x 1 =6; x 2 =9; x 3 =12; x 4 =15
p 1 =0,3; p 2 =0,3; p 3 =0,1; p 4 =0,3

Для сгруппированных данных остаточная дисперсия - средняя из внутригрупповых дисперсий:

Где σ 2 j - внутригрупповая дисперсия j -й группы.

Для не сгруппированных данных остаточная дисперсия – мера точности аппроксимации, т.е. приближения линии регрессии к исходным данным:
где y(t) – прогноз по уравнению тренда; y t – исходный ряд динамики; n – количество точек; p – число коэффициентов уравнения регрессии (количество объясняющих переменных).
В этом примере она называется несмещенная оценка дисперсии .

Пример №1 . Распределение рабочих трех предприятий одного объединения по тарифным разрядам характеризуется следующими данными:

Тарифный разряд рабочего Численность рабочих на предприятии
предприятие 1 предприятие 2 предприятие 3
1 50 20 40
2 100 80 60
3 150 150 200
4 350 300 400
5 200 150 250
6 150 100 150

Определить:
1. дисперсию по каждому предприятию (внутригрупповые дисперсии);
2. среднюю из внутригрупповых дисперсий;
3. межгрупповую дисперсию ;
4. общую дисперсию.

Решение.
Прежде чем приступить к решению задачи необходимо выяснить, какой признак является результативным, а какой – факторным. В рассматриваемом примере результативным признаком является «Тарифный разряд», а факторным признаком – «Номер (название) предприятия».
Тогда имеем три группы (предприятия), для которых необходимо рассчитать групповую среднюю и внутригрупповые дисперсии :


Предприятие Групповая средняя, Внутригрупповая дисперсия,
1 4 1,8

Средняя из внутригрупповых дисперсий (остаточная дисперсия ) рассчитаем по формуле:


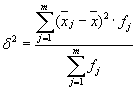
где можно рассчитать:
либо:


тогда:
Общая дисперсия будет равна: s 2 = 1,6 + 0 = 1,6.
Общую дисперсию также можно рассчитать и по одной из следующих двух формул:

При решении практических задач часто приходится иметь дело с признаком, принимающим только два альтернативных значения. В этом случае говорят не о весе того или иного значения признака, а о его доле в совокупности. Если долю единиц совокупности, обладающих изучаемым признаком, обозначить через «р », а не обладающих – через «q », то дисперсию можно рассчитать по формуле:
s 2 = p×q

Пример №2 . По данным о выработке шести рабочих бригады определить межгрупповую дисперсию и оценить влияние рабочей смены на их производительность труда, если общая дисперсия равна 12,2 .

№ рабочего бригады Выработка рабочего, шт.
в I смену во II смену
1 18 13
2 19 14
3 22 15
4 20 17
5 24 16
6 23 15

Решение . Исходные данные

X f 1 f 2 f 3 f 4 f 5 f 6 Итого
1 18 19 22 20 24 23 126
2 13 14 15 17 16 15 90
Итого 31 33 37 37 40 38

Тогда имеем 6 группы, для которых необходимо рассчитать групповую среднюю и внутригрупповые дисперсии.
1. Находим средние значения каждой группы .







2. Находим среднее квадратическое каждой группы .







Результаты расчета сведем в таблицу:
Номер группы Групповая средняя Внутригрупповая дисперсия
1 1.42 0.24
2 1.42 0.24
3 1.41 0.24
4 1.46 0.25
5 1.4 0.24
6 1.39 0.24

3. Внутригрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака в пределах группы под действием на него всех факторов, кроме фактора, положенного в основание группировки:
Среднюю из внутригрупповых дисперсий рассчитаем по формуле:


4. Межгрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него фактора (факторного признака), положенного в основание группировки.
Межгрупповую дисперсию определим как:

где


Тогда

Общая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него всех без исключения факторов (факторных признаков). По условию задачи она равна 12.2 .
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:

Определяем эмпирическое корреляционное отношение:

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0.3 0.5 0.7 0.9 В нашем примере связь между признаком Y фактором X слабая
Коэффициент детерминации.

Определим коэффициент детерминации:

Таким образом, на 0.67% вариация обусловлена различиями между признаками, а на 99.37% – другими факторами.
Вывод : в данном случае выработка рабочих не зависит от работы в конкретную смену, т..е. влияние рабочей смены на их производительность труда не значительное и обусловлено другими факторами.

Пример №3 . На основе данных о средней заработной плате и квадратах отклонений от её величины по двум группам рабочих найти общую дисперсию, применив правило сложения дисперсий:

Решение:
Средняя из внутригрупповых дисперсий

Межгрупповую дисперсию определим как:


Общая дисперсия будет равна: 480 + 13824 = 14304